Solving Trigonometric Equations on a Specified Interval 2

Helloo, this is mandeep! Today's class we learned about how to solving trigonometric equations on a specific interval 2. We solved some examples and find out how to solving theta(Θ) over the interval.
For example:- 2sin ² Θ = 3sinΘ - 1 over the interval 0 ≤ Θ ≤ 2π

To solve this equation ,we have to know how to do factors.(find two factors that when we multiply to 2 is + and if we add will be -).
2sin ² Θ = 3sinΘ - 1
2sin ² Θ - 3sinΘ + 1=0
(2sinΘ-1)(sinΘ - 1)=0

(2sin Θ-1)=0 and (sinΘ-1)=0

2sinΘ=1 and sinΘ=1

sinΘ=1/2 and sinΘ=1

sin 30° sin 90° = π/2
sinΘ is + in Q1 and Q2,draw a diagram and reference angle of 30°

Q1 : Ref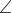 = Rel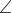 =π/6 OR 30°

Q2: π- π/6 = 5π/6

So answer of this equation is Θ = π/6 , π/2 , 5π/6

Note: If we need to calculator, make sure to set it to radians or degree .