Circular Permutations

- are arrangements of elements in a circular pattern.

Formula:

Example 1:

• In how many ways can 5 people be seated around a circular table?

n=5

Formula: (n-1)!

(5-1)!

4!

4.3.2.1

= 24

• In how many ways can 8 girls be seated in a dinner table?

n=8

Formula: (n-1)!

(8-1)!

7!

= 5,040

* There are two cases of circular permutation;*

(a) If clockwise and anti clock-wise orders are different, then total number of circular-permutations is given by (n-1)!

(b) If clock-wise and anti-clock-wise orders are taken as not different, then total number of circular-permutations is given by (n-1)!/2!

Example 2:

How many necklace of 12 beads each can be made from 18 beads of different colours?

clock-wise and anti-clockwise arrangement s are same.

total number of circular–permutations:

¹⁸P₁₂/2x12

=18!/(6 x 24)

= 4.45x10 to the power of 13

* Some permutation problem have restrictions that affect the

answer and the process of solving it

• In how many ways can 8 people be seated around a circular table if Edgar and EJ refuse to sit next to one another?

STEP 1: Calculate total arrangements that is given in the problem.

n=8

Formula: (n-1)!

(8-1)!

7!

=5040

STEP 2: Calculate the number without following the restrictions, for this calculate the number when Edgar and Ej sit together.

*Edgar and Ej is going to be a one group because they sit together, so it makes (2!)

*added to the people left. (6!)

= 7!

(n-1)

(7-1)! =6!・2! = 1440

STEP 3: Calculate the number following the restrictions, for this calculate the number when Edgar and Ej is not sitting together.

* Subtract the total number of arrangement and the total number when Edgar and Ej is sitting together .*

5040-1440 = 3600

Permutations with Case Restrictions

Example 1:

*In how many 5 letter “words” are possible using the letters in BUFFALO?

*used the dash method

*count how many letters are their in the word BUFFALO. so theres 7 words.

*find letters that are repeated and divide the total number of with the number of letters that are repeated. and theres 2 repeated letters.

(7・6・5・4・3) ÷ 2 = 1,260

• Theres a set of basket of fruits being arranged in a cabinet. The first set has 3 oranges, the second has 4 bananas and the third set has 5 apples. In how many ways can the basket of fruits can be arranged if they should be kept in a same cabinet together?

○ - oranges

▲- apple

～ - bananas

～～～～ 4!

▲▲▲▲▲ 5!

○○○ 3!

*multiply all the number of quantity of the given number of fruits and the number of item that are given.

4! ・ 5! ・3! ・3! = 103,680

Hi Everyone!

1. Problem: What is the probability of rolling a 3 on a die (plural, dice).

Solution: On a fair die (not the kind you play with in Vegas, where everything is rigged), there are six equally likely outcomes when you roll. Also, there is only one way to get a 3. By the definition of probability, P(3) = (1/6).

A permutation of a set of objects is an arrangement of the objects in certain order. For example, take the set of four objects {pepperoni, sausage, onions, mushrooms}.

They can be arranged on a pizza many different ways. Below are a few of the
ways.

pepperoni, sausage, onions, mushrooms sausage,
onions, mushrooms, pepperoni onions, mushrooms, pepperoni,
sausage mushrooms, pepperoni, sausage, onions pepperoni,
sausage, mushrooms, onions There are some more, but we won't list
them.

To find the number of different arrangements of the set we select a first
choice; there are 4 possible choices.

Now we take a second choice; there are 3 choices. Now pick a third choice; there are 2 choices.

Finally, there is 1 choice for the last selection. Thus, there are 4
* 3 * 2 * 1 or 24 different ordered arrangements of the toppings.

This product can also be written as 4! (read: 4-factorial).
The total number of permutations of a set of n objects is given
by n!. Example:

1. Problem: 5!
Solution: 5 * 4 * 3 * 2 * 1
120
When you have a set
of objects and only want to arrange part of them, you have a permutation of
n objects r at a time.

For example, if you have 6 toppings for a pizza, and a customer calls and tells you to put any 3 toppings on the pizza, you might want to know how many different pizzas you can make. You can select the first topping in 6 ways, the second in 5, and the third in 4. As we learned above, this can be written as 6 * 5 * 4. There is a theorem that tells us about a formula for the situation above. It says the number of permutations of a set of n objects taken r at a time is given by
the following formula: nPr = (n!)/(n - r)!.

Example:

2. Problem: If a school has lockers with
50 numbers on each combination
lock, how many possible
combinations using three
numbers are there.
Solution: Recognize that n, or the number
of objects is 50 and that r, or
the number of objects taken at one time is
3. Plug those numbers in the permutation
formula.
50!
50P3 = --------
(50 - 3)!
Use a calculator to find the
final answer.
117600
Things are immensely simplified when you can repeat the objects. For example, if you are making license plates with only 4 letters on them, and you can repeat the letters, you can take the first letter from 26 options, the same for the second, third, and fourth. Therefore, there are 264 or 456976 available
license plates using 4 letters if you can repeat letters. There is a special
theorem that tells us the number of arrangements of n objects taken
r at a time, with repetition is given by nr.
Example:

3. Problem: How many 4 digit license plates
can you make using the numbers from
0 to 9 while allowing
repetitions.

Solution: Realize there are 10 objects
taken 4 at a time. Plug that
information into the formula for
repeated use.
104
10000

Applications of Exponential Functions

Today in class we learned about Applications of Exponential Functions.

There are three Formula's you should know

Formula for Growth and Decay

A=Pe^rt Where: A = Final amount, P = Initial amount, r = rate/constant, and t = time

Formula for Compound Interest

A=P(1+r/n)^rt Where: A - Final Amount, P = Inital Amount, r = Rate, n = number of compounds per year, and t = time.

Formula for Continuous Compound Interest

A=Pe^rt Where: A = Final amount, P = Initial amount, r = rate/constant, and t = time

Now that we know those questions lets do a couple questions.

Example 4 from the Exponents and Logarithms booklet.

A $15000 investment earns interest at the annual rate of 7.6% compounded quarterly.

Determine the value of the investment after 9 years

and the amount of interest earned after 9 years.

1. State what is given.

Initial amount = 15000

Rate = 7.6% = 0.076

time = 9 years

and n = 4

2. Plug in your values into your formula.

A= 15000(1+ 0.076/4)

A=15000(1.019)^36

The ^36 came from multiplying 9 by 4 since you are looking for the investment after 9 years and you are being compounded quarterly(4)

3.A= 29536.70

You have found out that the value of your investment is $29536.70 after 9 years. Now you want to find out the interest earned after 9 years.

4. Interest earned = Final Amount - Initial Amount

5. 29536.50 - 15000 = $14536.7

Example 2

Bacteria are growing according to y = A * 2^x. If the initial bacteria count is 10,000 determine how many hours it will take for the bacteria count to triple.

1. State what is given

A=10,000

final amount = 30000( since you know that the amount your looking for is tripled you mulitply your original initial amount which is 10,000)

time=x=?

The formula you would use would be A=Pe^rt

2. plug in your amounts

30000=10,000 * 2^x

divide both sides to get 2^x by it's self

3. 3=2^x

you can't make bases the same so you have to put logs in the front

4. log3 = log2^x

divide by log 2^x to get the x by it's self.

5. x= log3/log2

6. now you type in log3/log2 in you calculator and you should get 1.6 rounded off .

Thanks for reading and just a reminder that we have a test on Friday so start studying!

Logarithmic Theorems II

Hello,

        These Are the Logarithmic Simplification Steps
     1. Rearrange the terms- moving all negative to the end    
     2. Exponent Law- Coefficients become exponents (move to the top)
     3. Multiplication Law- Addition becomes multiplication
     4. Division Law - Subtraction becomes division
     5. Fractional Exponents become roots

     Change of Base Formula:

       Note:
            - Calculators are based on 10
            - If not, we assume base 10
            - if it isn't on base 10, we will need to change the base to 10 so we can evaluate logarithms using the 
             change of base formula

Example 1:

     
Example 2:

Example 3 (Evaluate to 4 Decimal Places)

That's all and Have a great night!!!!

Logarithmic Theorems 1

Laws of Logarithims

Division Law: loga M/N = loga M - loga N For Division Law switch the division into subtraction

Multiplication Law: loga MN = loga M + loga N For Mulitiplication Law switch the multiplication into

addition

N

Exponent Law: loga M = N loga M Just put the N to the Front

Logarithmic Expansion Steps

1. Roots become fractional exponents

2. Division Law - Division becomes subtraction

3. Multiplication Law - Multiplication becomes addition

4. Exponent Law - Exponents become coefficients (move to the front)

Expand

logb Division becomes subtraction

= logb - logb x Roots become fractional exponents

2 1/2

= logb (x - 1) - logb x Exponents become coefficients (move 1/2 to the front)

2

=1/2 logb (x - 1) - logb x This could be simplified further

= 1/2[logb (x+1) + logb (x-1)] - logb x Multiply the brackets

= 1/2 logb (x+1) + 1/2 logb (x-1) - logb x Final Answer

Here is another example:

If logb 2= 0.3010 , logb 3= 0.4771 , and logb 5 = 0.6990 , then:

logb 20/3 = Division becomes subtraction

= logb 20 - logb 3 logb 20 can be simplified

= logb (5)(4) - logb 3 4 can be simplified further

= logb (5)(2)(2)- logb3 Multiplication becomes addition

= logb 5 + logb 2 + logb 2 - logb 3 Switch with the other values

= 0.6990 + 0.3010 + 0.3010 - 0.4771 Solve

= 0.8239 Final Answer

I hope this helped. Brendan

October's Halll of Famer

Please cast your vote for the Hall of Famer of October.

Exponential functions

Hey guys what's up ! Mehtab here. I'm going to try to solve some exponential functions and i hope that it might help you as well. These functions needs to be moved vertically or horizontally whenever required. We have done the transformation unit, so this is not going to be a hard one, I guess. So,

Important :

.

For example:

Let's start by using table of values, the easy method.

After that you graph it, simple as that. There is no horizontal asymptote, so y=0.

Another example:

Table of values:

No horizontal asymptote, so y=o.

(B)

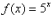
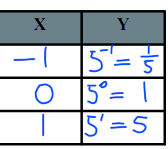
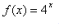Now, graph and then move all the points to the right by 3, resulting in the end of your question. I hope you all got it.