Hi this is Karla, Last wednesday, we start a new unit which is Unit 2 Transformations. The first topic that we learned from this is Translations.

It has two shifting rules:

• Vertical Translations

y=f(x)+k graph up k units

y=f(x)-k graph down k units

• Horizontal Translations

y=f(x-h) graph right h units

y=f(x+h) graph left h units

example: y = x^{2 and} y = x² + 1

Note:

* Always read h values as opposite *

example:

h value will graph moving 2 points to the right . and k value will graph 3 points moving up.

General Solutions of Trigonometric Equations 2 (sept.22/2011)

Hi this is orit , and im here to go over our latest lesson!

There are many parts to this lesson and they must be done carefully

For example..
sin3Ө=-√2/2

Our first step would be to rationalize √2/2, and we will get -1/2.
Sin = O/H
When we have -,+ 1 as a opposite and 2 as a hypotenues, 45 degrees will be the angle which is π/4.
Sin is negative in Q3 and Q4, that is where the right angle triangles will be placed.



We know that our angle is 45 degrees and its in QIII and QIV, so our next step would be to add π to π/4 and subtract 2π from 5π/4 which equals to 7π/4

Next , we will be adding our [5π/4 + 2kπ, 7π/4+2kπ]

In order for us to get rid of the 3 , we must multiply the denominators by 3.
3Ө= 5π/4x3 + 2kπ/3, 7π/4x3 +2kπ/3

The final answer is

[Ө= 5π/12 + 2kπ/3, 7π/12 +2kπ/3 , where K€I]

Solving Trigonometric Equations on a Specified Interval 2

Helloo, this is mandeep! Today's class we learned about how to solving trigonometric equations on a specific interval 2. We solved some examples and find out how to solving theta(Θ) over the interval.
For example:- 2sin ² Θ = 3sinΘ - 1 over the interval 0 ≤ Θ ≤ 2π

To solve this equation ,we have to know how to do factors.(find two factors that when we multiply to 2 is + and if we add will be -).
2sin ² Θ = 3sinΘ - 1
2sin ² Θ - 3sinΘ + 1=0
(2sinΘ-1)(sinΘ - 1)=0

(2sin Θ-1)=0 and (sinΘ-1)=0

2sinΘ=1 and sinΘ=1

sinΘ=1/2 and sinΘ=1

sin 30° sin 90° = π/2
sinΘ is + in Q1 and Q2,draw a diagram and reference angle of 30°

Q1 : Ref = Rel =π/6 OR 30°

Q2: π- π/6 = 5π/6

So answer of this equation is Θ = π/6 , π/2 , 5π/6

Note: If we need to calculator, make sure to set it to radians or degree .

Monday, September 19 - Solving Tirgonometric Equations on a SPecified Interval 1

What we did on the Monday class was a review of grade 11, just that we were solving with the 3 Special Triangles :

(they don't want to go in the right place)

How to solve for Ө:

1) Determine the reference angle
2)Select possible quadrant(s) using CAST rule,(Q1 Q2 Q3 Q4)
3)Check the interval given

4)State value(s) for Ө in degrees or radians.

Ex: 2SinӨ=1 interval 0-360

1st step: Solve for SinӨ
(I guess everyone knows how to solve this :P )
SinӨ= 1/2 = O/H (so we know its a 30* angle)

2nd step: draw a diagram (or not/or its given) and look in which quadrant it could be by using CAST rule, here we know it can be in Q1 and Q2 so we gonna get 2 equations

3rd step: calculate Ө in each possible quadrant(s) so Q1=ref. angle(now 30*)
Q2=180* - ref. angle (30*)
so we get the answers of Ө in Q1=30*
and in Q2=150*

Hope it is readable because my english is not so good :) ( in writing something down)

And Good Morning :P

Friday, September 16 - Special Angles and Trignometric Functions 2

Hi guys its Ishu! On fridays class we started off by going through examples and questions from previous exercises that were assigned for homework and went more in depth with special angles and trigonometric functions. We applied the skills we learned from previous lessons and used them to solve equations. For example:




1st step- Separate everything and figure out the angle that is being referred to. You can also draw out the unit circle for each one if it helps you.

eg. sin(pi/2): (pi/2)=90° aka sin90°
sin(pi/6): (pi/6)=30° aka sin30°
cos(pi/3): (pi/3)= 60° aka cos60°
tan(pi/4): (pi/4)= 45° aka tan45°

2nd step- Make reference to or draw out the quadrantal angles/special triangles for each one and and figure out the exact values.

eg. for sin(pi/2): We'll use our knowledge of quadrantal angles.




By using this diagram, we can figure out that sin (pi/2) = 1 since sin =y and the value for y in P (0,1) is 1.


eg. for sin (pi/6): we know thats the same thing as saying sin of 30°, so we draw the special triangle for 30°, label each side and use SOH to figure out the exact value.




Therefore sin(pi/6) = 1/2 since the opposite side is = 1 and the hypotenuse is = 2.

You should get:
sin(pi/2)=1
sin(pi/6)=1/2
cos(pi/3)=1/2
tan(pi/4)=1

3rd step: Substitute the equation for the exact values you've found and solve.

= 1 [1/2 + 1/2 ]= 1

Therefore,

1 [1/2 + 1/2] =1
1 [2/2] =1
2/2= 1
1=1

*We know that our answers were right because the left side equaled the right side*

And we've finally solved the problem.. YAY. alright i hope this helped and dont forget to do the homework that was assigned as well as the assignment! See you all on Monday, good luck and enjoy your weekend :) ............and just for kicks, someone wanna do my homework?

Special angles and the trigonometric functions 1

Today in the class we learn more briefly about the special angles of the Unit Circle.Most angles on the Unit Circle are basically multiples of the special angles which are 0° ,30°(π/6),45°(π/4) ,60° (π/3) ,90°(π/2).We also learned How to fill out the chart of special angles.First special angles and quadrantal angles could be found using Reference Triangles which we learned in the last class.

Let say now you want to find the trig  values for 225°(5π/4). Look at the chart above and see which one has same denominator values in radian measure.In this case it is 45°(π/4).Copy down all the values of trig functions SinӨ ,CosӨ ,TanӨ.Keeping the CAST rule in mind you should know what are the signs of trig functions.225° angle is  found in Ouadrant 3. SinӨ and CosӨ are negative in Quadrant 3 and TanӨ is positive.Signs will change in some of the cases.Because Trig values signs are different in different quadrants.

We also learn how to find the coordinates for P(Ө).

Example.1

a) P(π/4)

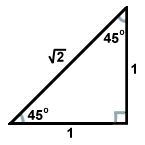
   To make it easy set up isosceles right triangle on the Unit Circle.It will look like this.

Find the SinӨ(π/4)  and CosӨ(π/4)

SinӨ= O/H and CosӨ=A/H

SinӨ =1/√2

CosӨ=1/√2

Therefore P(π/4) =(1/√2,1/√2).

Last thing we learn is finding exact values.

Ex no.2 

a) Tan 150°

It is kind of same as above example.

Set up the right triangle on unit circle.

find values of SinӨ and CosӨ Which are 1/2 and √3/2

TanӨ = SinӨ/CosӨ

= Which will give us 1/√2.

Mr P also told us to fill up the Unit circle. If you want to check if you did it right Click on the link below.

http://www.geocities.ws/petrinamaher/UnitCircle.GIF

Don't forget to do homework.
Ex.3,Questions 1,2,10-12 and worksheet.
See u all tomorrow.

If anyone can help?

On the worksheet for unit circle question 12 I got -11/ square root 125 now I know this isnt right because the square root cant be on the bottom but I cant remember how to change it

The Unit Circle

Hello, this is Harry Kainth, our lessons from the past two classes have been about the unit circle.

The equation of a unit circle is x^2 +y^2 = 1, another way to look at it is cos^2 θ + sin^2 θ = 1.

sorry I couldn't find any nice pictures like Stefan did.

We learned that the notation P(θ) denotes the terminal point. The terminal point is where the terminal arm of the angle θ intercepts the unit circle.

We solved questions where we were given the value of cosθ and had to find the values of sinθ and tanθ, also where we had the value of y and had to find the value of x and tanθ.

We also began learning about Special Angles and the Trigonometric Functions, which is about determining the exact values of trig. ratios for any multiples of 0°, 30°, 45°, 60° and 90°, and also 0, π/6, π/4, π/3 and π/2.

We were assigned a Unit Circle worksheet and questions from the exercise book to complete for tomorrows class.

Degree and Radian measure 2

Hi, this is Stefan. Today's lesson was a continuation of what we learned on Friday. We also got a new formula which is used to find the area of the sector. When plugging in theta, it must be in radians. So if in the question you are given the angle in degrees, you must convert it to radians before plugging it in the formula. The formula we mostly focused on today was . We were given two factors and were asked to find the third. Remember that we can always rearrange the formula to solve for any of the three factors. Homework was the worksheet "Degree and Radian Measure 2" and exercise 1, questions 3-5, 11,12.

Hope this helped!!!

A Helpful Video.

I have found a video that has given me a better understanding on Degrees and Radians.

http://www.youtube.com/watch?v=cLBKOYmHuDM

Hope It Helps :)

Pre-Cal Friday

The lesson on Pre-Cal last Friday was salty yet sweet. I find it salty because,the topic about coterminal angles was full of twists and turns,esp. with the pi part and the graphing part (the one with the rotation on it; until now i had a hard time answering it). On the other hand, i find the radian-degree part easy as a fried egg because,you'll just have to convert it vice versa.                           So,i implore your help,Mr.P and to you,guys to help me with the coterminal angles and the rotate-turn angle graph part. Thank you and have a nice day.