Pre-Calculus 40S Fall 2011 Section B: Conics

In mathematics, a conic section (or just conic) is a curve obtained by intersecting a cone (more precisely, a right circular conical surface) with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2.

Circle

The equations for circle are :

The General formula for circle is = Ax^2 + By^2 + Cx + Dy + E = 0

Distance

Distance Formula is :

It is use to find the distance between the points and with that we can find the radius of a circle given the points of it.
Midpoint

Midpoint formula:

We can use this formula to find the center of the circle.
Parabolas

There are vertical and horizontal parabolas.

Vertical Parabola

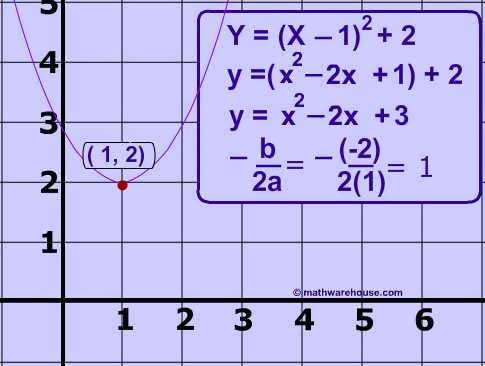
We already know that the vertical parabola has an equation of :
y = a((x-h)^ 2 ) + k

where a is the coefficient that is responsible for the horizontal size of the parabola and whether the parabola opens up or down
where h is read as opposite and is vertical symmetry and a point in x axis
where k is read as is and a point in y axis

Example:

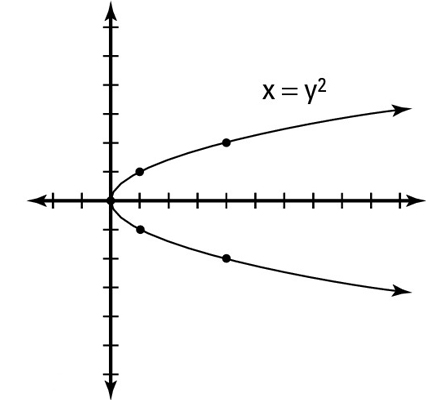
Horizontal Parabola.

Our normal parabola opens up or down, but this parabola opens to the left or right. The equation is:
x = a((y-k)^2) + h

Here's an simple equation and example of a Horizontal Parabola

Remember that in Vertical Parabola if a is positive the parabola goes up and down if negative and in Horizontal Parabola if a is positive it goes to the right and left if negative.

So that's mostly it.
Here's a circle, not an ordinary circle though. I don't know if you know this already. If you don't, look at the center of the circle and fixate your eyes at it then try looking at it closer then further, then closer, then further, over and over again. ;)