last post for 2011!!!

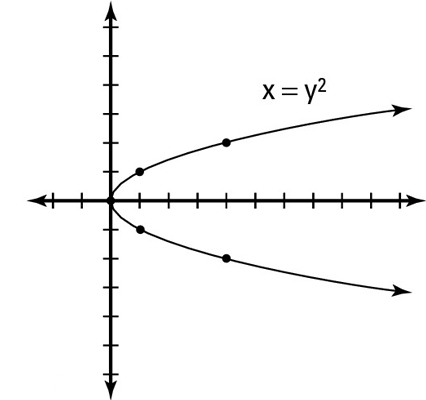
today we knew how to find the equation for a parabola

EX. find the equation for the horizontal parabola with vertex at 4,1 and passing through the point 2,5. you might want to label your given points h,k and x,y for you not to get confused.

use the formula (x-h)=a(y-k)^2 from here all you have to do is plug in the values and solve.


we also knew how to find the vertex of a parabola if we are given an equation and a passing point.

EX. if the parabola y^2+x-6y-m=0 passes through the point (-3,5) find the vertex.

first step is to label the given passing point x and y for you not to get confused, next is to plug -3 to the x in the equation and 5 to the y's in the equation and solve for m. in this case your m shall equal to 8. next thing for you to do is plug your 8 for m to the equation. DO NOT PLUG -3 AND 5 TO YOUR x AND y, complete the square and solve algebraically. your vertex should be at (1,3). that's all and thank you.

Conics

In mathematics, a conic section (or just conic) is a curve obtained by intersecting a cone (more precisely, a right circular conical surface) with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2.

Circle




The equations for circle are :


The General formula for circle is = Ax^2 + By^2 + Cx + Dy + E = 0

Distance

Distance Formula is :



It is use to find the distance between the points and with that we can find the radius of a circle given the points of it.
Midpoint

Midpoint formula:



We can use this formula to find the center of the circle.
Parabolas



There are vertical and horizontal parabolas.

Vertical Parabola

We already know that the vertical parabola has an equation of :
y = a((x-h)^ 2 ) + k

where a is the coefficient that is responsible for the horizontal size of the parabola and whether the parabola opens up or down
where h is read as opposite and is vertical symmetry and a point in x axis
where k is read as is and a point in y axis

Example:




Horizontal Parabola.

Our normal parabola opens up or down, but this parabola opens to the left or right. The equation is:
x = a((y-k)^2) + h

Here's an simple equation and example of a Horizontal Parabola



Remember that in Vertical Parabola if a is positive the parabola goes up and down if negative and in Horizontal Parabola if a is positive it goes to the right and left if negative.

So that's mostly it.
Here's a circle, not an ordinary circle though. I don't know if you know this already. If you don't, look at the center of the circle and fixate your eyes at it then try looking at it closer then further, then closer, then further, over and over again. ;)



It moves right? :O lool



1 more day to goooo!! :D You know what it is ;P




4 more days 'til Christmas! Merry Christmas Everyone. ;)




-Paul

November Hall of Famer

And the winners are:

1 - Roxanne - 7 points - 3 bonus points
2 - Carjelu and Gurvinder - 6 points - 2 bonus points each
3 - Karla - 4 points - 1 bonus point

Sample Space

Hi fellow PreCal classmates! This is Paulene J Our blog site is not up to date anymore just because I forgot to post mine on time & I'm very sorry about that!

Anyways.. last December 06, we started a new lesson called Sample Space. It’s a very short topic under the Probability Chapter/Unit.. and here’s a recap! J

Sample Space refers to the complete set of all possible outcome. These are often represented using tree diagrams and ordered pairs. The probability that a specific event will occur can be described as.. P(E) = Success ÷ (sample - space)

There are also two events that can occur;

- Dependent events is when the outcome of one event affects the outcome of a second event.

- Independent events is when the outcome of one event does not influence the outcome of a second event.

November Hall of Famer

Please cast your votes (under comments) for the Hall of Famer of November.
Thank you.

Binomial Theorem

Hey fellow students ! last Friday we talk about binomial theorem which is discovered by a very smart man whose name is pascal . This theorem is basically a much quicker or less slower way of expanding a binomial expression that is raised to a very high power . To help us understand it i try to look for a site that can explain it better than me . So this what i found

http://www.math10.com/en/algebra/probabilities/binomial-theorem/binomial-theorem.html.

and i also found a very helpful video (: i hope this will help you guys even more .
http://www.youtube.com/watch?v=bMB8qDYa8N0

Combinations

The formula for the number of possible combinations of r objects from a set of n objects:



Example: How many different committees of 4 students can be chosen from a group of 15?

There are 1365 different committees.

	If the order doesn't matter, it is a Combination.
	If the order does matter it is a Permutation.

1.) Combinations with repetition

Let us say there are five flavors of icecream: banana, chocolate, lemon, strawberry and vanilla. You can have three scoops. How many variations will there be?

Let's use letters for the flavors: {b, c, l, s, v}. Example selections would be

• {c, c, c} (3 scoops of chocolate)
• {b, l, v} (one each of banana, lemon and vanilla)
• {b, v, v} (one of banana, two of vanilla)

(And just to be clear: There are n=5 things to choose from, and you choose r=3 of them.
Order does not matter, and you can repeat!)

where n is the number of things to choose from, and you choose r of them
(Repetition allowed, order doesn't matter)

(5+3-1)!	=	7!	=	5040	= 35
3!(5-1)!		3!×4!		6×24

2.) Combinations without repetition

where n is the number of things to choose from, and you choose r of them
(No repetition, order doesn't matter)

By: Roxanne Ching