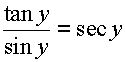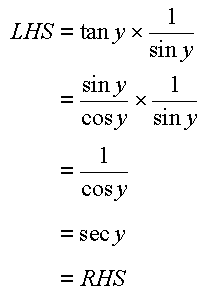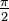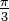Double Angle Trigonometric Identities

Hey everyone!

For today's lesson, we studied Double Angle Trigonometric Identities which is very simple and I know that a lot of you have no troubles with it. So I'll be very brief on explaining how this one works.

Basically, this lesson is very similar to our previous lessons. The process and steps are the same.

The only thing you have to do is to find the equivalent value of the given identity from your formula sheet and substitute it to the original function.

Here are the basic Double Angle Trig Identities:

You can have different forms of equations but it will end up with the same answer as long as you don't mess up. Always choose the easier ones.

On some questions, you'll be ask to find the exact values of sin, cos or tan. Always follow the simple steps. Once you get the equation, set alpha and beta. Solve and find the value of trig identity. You need to use CAST rule, Special triangles and Pythagorean theorem to find the values depending on what you are told to look for.

As long as you know the equivalent of each set of identities(which is in our formula sheet), you'll be fine.

Hope this helps!

K bye.

Homework

Hi,Does anybody know what is the homework for today? Please reply and Thank You.

-David

Sum and Difference Part 2

Hi Guys..

Since there is no new topic and we only did exercises in the booklet... I'm just gonna answer the last question it this topic...

Hope this helps...

Sum and Difference Identities Part One

HI!!! Today in precal we studied about sum and difference identities part one.
lets go to the first example

ex. sin 7pie/12 first step that you need to do is to set an equation that will equal to 7pie/12
the equation that you need to have is either addition or subtraction. note that there is many possible equation for the example given.

sin 7pie/12=sin(4pie/12+3pie/12) *SIMPLIFY*
=sin (pie/3+pie/4) *LABEL as ALPHA and BETA*
alpha beta
at this point you have to have your formula sheet with you. The formula for this equation would be sin(A+B)= sinAcosB + cosAsinB meaning you should have sin pie/3 x cos pie/4+cos pie/3 x sin pie/4 what you have to do next is to find the exact values of these trigonometric values which means you need to use the special triangles and the cast rule. therefore you should have...





your final answer should be as stated in the image above. don't do anything to your final answer leave it as it is.

at some point you will be given csc 19pie/12. the trick to this is to solve it as sin 19pie/12 and just get the reciprocal of your final answer.

K BYE!!! ahaha...

TRIGONOMETRIC IDENTITIES

HELLO!

We started on discussing about trigonometric identities. It is basically proving that both sides of an equation are equal. To help you do this, you should always consider the following identities:

sin θ	=	1 csc θ		csc θ	=	1 sin θ
cos θ	=	1 sec θ		sec θ	=	1 cos θ
tan θ	=	1 cot θ		cot θ	=	1 tan θ

a)	sin²θ + cos²θ	=	1
b)	1 + tan²θ	=	sec²θ
c)	1 + cot²θ	=	csc ²θ

tan θ =

sin θ cos θ

cot θ =

cos θ sin θ

For example,

Answer

We express everything in terms of sin y and cos y and then simplify:

Just play around with the equation until you end up having both sides equal. BUT STILL MAKE SURE THAT YOU ARE PLAYING IT RIGHT!

More examples

Happy Birthday Mr.P

Have a Happy Birhtday!

Hi guys! Last friday, we were finishing up the topic about Sinusoidal Functions.

Let's take a recap about how to create equations for sinusoidal functions.

1. First, we have to find the middle axis (this will be d-value)
   
2. Find the amplitude (this will be the a-value). The easiest way to find the amplitude is to count from the middle axis to the highest point the graph is reached)
   
3. Determine the period and then calculate the b-value.
   
4. Identify the type of original wave (it's either y=sinx or y=cosx)
   
5. Create the first equation using the a, b, c and d values
   
6. Create the second and third equations including the a,b,c and d values.

So for example.

1. The middle axis will be at 0 which makes the d value = 0

2. Amplitude = 1

3. Period = 2π so b value will equal to 1

4. The type of original wave for this graph would be y=cosx

5. So now, we will create our three equations

I. y=cosx

II y=sin(x-)

iii. y=-sin(x+)

Note: Your goal is to manipulate the type of function you`re working with for the second and third equations by making it mask the original equation. Also, when creating the two other equations after determining the equation for the sinusoidal function, the two equations have to be the opposite or the other function that was not the original. If the original function was cos, then the two other equations would be sin. And vice versa.

The other thing we learned about is solving functions which involves some of the stuff we learned from Unit 1: circular functions

For example: p(x)=-cos(x+5) - 2

Things to keep in mind: special triangles and quadrantals.

p(0) = - cos(0+5) - 2 I put x to 0

= - cos(5) - 2

Multiply 5 by which becomes ⁵

= -cos ⁵ - 2

** Cos = adj/hyp so ⁵ = 1/2 but since cos was -'ve then 1/2 would be -'ve as well.

= -1/2 - 2

= -1/2 - 4/2

= -5/2

Quick reminder: Every lesson we learned will be helpful to the next unit and so on.

Anyways, hope everyone had a greaaat weekend!! :)

Creating Equations for Sinusoidal Functions

Hi! This is kyle and we learned about how to create equations for sinusoidal functions.

So, these are the things that you need to know first..
a - amplitude
b - |b|
c - horizontal shift
d - vertical shift
because those are the ones the will be going to be plugged in f(x) = a sin b(x - c) + d or f(x) = a cos b(x - c) + d

moving on..

STEPS ON FINDING THE EQUATION FOR SINUSOIDAL FUNCTIONS:
1.) Find the middle axis (d - vertical shift) of the graph. It is the one that determines the up and down shifting of the graph.
2.) Determine the amplitude.
3.) Determine the period. Then, you can now solve for the |b| value.
4.) Identify the type of wave. It is only either sin or cos.
5.) Determine the horizontal shift by counting how many radians it shifted to the left or right.
6.) Create the equation by plugging the a,b,c,d value in f(x) = a sin b(x - c) + d or f(x) = a cos b(x - c) + d

Absolute Value Function

Hello fellow classmates! This is Paulene :D Yesterday, we learned what an Absolute Value Function is and how to graph it.

This is the Parent Graph of all absolute value functions or "Basic Shape" f(x) = |x|

It has the same V-shape, but they can be wider or narrower. They might have their vertex somewhere else other than the origin, and they might open downward instead of upward.



Shifted Shape: f(x) = |x-h| + k :: You read k as is and h as opposite.

How to graph by "reading" an Absolute Value function:
1. Read k values as is. If k is positive, the graph shifts up.
If k is negative, the graph shifts down.
2. Read h values as opposite. If h is positive, the graph shifts left.
If h is negative, the graph shifts right.

Eg. (f)x = |x+1| + 2 :: The graph will shift 2 up, 1 to the left.

How to graph an Absolute Value Function using a table:

1. Choose an x-value
2. Sub in the value for x in the equation
3. Simplify
4. The answer is the now the y-value
5. Repeat Steps 1-4 for 2-4 more x-values and sketch the function.

Eg. (f)x = |x+2|

x value - y value

0 - |0+2| = 2
1 - |1+2| = 3
2 - |2+2| = 4
-1 - |-1+2| = 3
-2 - |-2+2| = 0

Reciprocal Functions 2

Hi guys! Last Thursday we learned How to Graph Reciprocal Trigonometric Functions.

How to graph:

• ( when period is )

1. Graph the basic sin x shape.

2. Place vertical asymptotes in x-intercept where reciprocated sin x is undefined ( 0, , )

3. Flip the remaining curves.

• (when the period is )

1. Graph the basic cos x shape.

2. Place vertical asymptotes where reciprocated cos x is undefined ( , )

3. Flip the remaining curves.

• ( when period is )

1. Create a table of values using quadrantals and 's ( refer to booklet )

2. Since , place vertical asymptotes on 0, , .

Reciprocal Function

Hi! Paul here. Yesterday's lesson was about Reciprocal Function. We learned it from grade 11 and yesterday was like a review so I made a little something for this topic. Click here. It shouldn't be that hard because we only had the basics yesterday. All we need to do is to find the asymptotes then graph the reciprocal function (use table of values because the numerator isn't always going to be 1). That's all. Don't forget to check the link up there. ^ ;)

Hey there classmates ! this is carjelu and i will talk about symmetry, reflections and inverses.

So we learned today that if you replace x with -x in the equation y = f(x) the graph will be reflected in the y-axis.

For example:

f(x) = x³

f(-x) = (-x³)

Take note that the reflection in y-axis makes x-value negative !

When y is replaced with -y in the equation of a function y = f(x) , its graph will be reflected in the x-axis.

For example:

f(x) = x²

-f(x) = (x²) -> f(x)= -(x²)

Take note that reflection in the x-axis make y-values negative !

When x is interchanged with y in the equation of a function y= f(x), its reflected in the mirror line y = x. This is called an inverse function.

we also learned the steps on how to find the inverse equation:

1. Replaced f(x) with y.
2. Switch x and y.
3. Solve for y.
4. Replace y with f-1(x).

We were given the function of f(x) = 2x + 2 and we have to graph it and its inverse. Then we determine the algebraically equation of the f-1(x).

the black line is called the mirror line where x = y

(1,4) => (4,1)

(0,2) => (2,0)

(-1,0) => (0,-1)

f(x) = 2x + 2

y = 2x + 2

x = 2y + 2

x - 2 / 2 = 2y / 2

y = x - 2 / 2

f-1(x) = 1x/2 - 1

Take note that reflection in the mirror line switch x and y values !

Transformations Effect on Graph

-f(x) reflection in x-axis

f(-x) reflection in y-axis

f-1(x) reflection in y=x

Symmetry

a graph is said to be symmetrical through an axis or the origin if either side is the mirror image of the other .

A function f(x) is even if for any value "x" f(-x) or -f(-x) = -f(x). Even functions are symmetric about the y-axis. This mean that positive and negative x-values result in the same y-value.Even functions would be symmetrical between quadrants I and II or quadrants III and IV.(example is vertical parabola)

A function f(x) is odd if a any value "x" f(-x) = -f(x) or f(x)=-f(-x). Odd functions are symmetric about the origin. This means that positive and negative x-values result in different y-values. Odd functions would be symmetrical between quadrants I and II or quadrants III and IV.(example is a vertical cube)

that would be it :D bye . . . .

Hall of Famer for September

Please cast your votes for the hall of famer of the month.

September 29, 2011

Hi, this is roxanne and our latest lesson was about stretches and compressions.

y=af(x) stretches vertically a is greater than 1.
y=1/af(x) compresses vertically 1 is greater than a.

For example, f(x)= x3 and 2f(x),

The red one is being times by 2 and x stays the same.








You could graph this by:



y=f(bx) compresses horizontally b is greater than 1

y=f(1/bx) stretches horizontally 1 is greater than b

( "read b values as opposite")

For example, f(x)=x2 and f(1/2x),

The red one is being times by two since the opposite of 1/2 is two. And this time y stays the same.

You could graph this by:

I hope everyone had a good weekend! :) Bye.